Why Are Convex Optimisation Problems Considered to Be Easy to Solve
Convex Problems
-
Mathematical programming problems
-
Convex optimization problems
-
Optimality
-
Equivalent problems
-
Complexity
Mathematical programming problems
Definition
A mathematical programming problem is one of the form
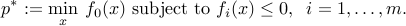
-
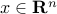 is the decision variable;
is the decision variable; -
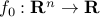 is the objective function;
is the objective function; -
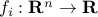 ,
, 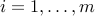 represent the constraints;
represent the constraints; -
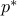 is the optimal value.
is the optimal value.
The term "programming" (or "program") does not refer to a computer code. It is used mainly for historical purposes. A more rigorous (but less popular) term is "optimization problem". The term "subject to" is often replaced by a colon.
By convention, the quantity 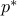 is set to
is set to 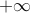 if the problem is not feasible. The optimal value can also assume the value
if the problem is not feasible. The optimal value can also assume the value 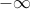 , in which case we say that the problem is unbounded below. An example of a problem that is unbounded below is an unconstrained problem with
, in which case we say that the problem is unbounded below. An example of a problem that is unbounded below is an unconstrained problem with 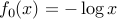 , with domain
, with domain 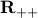 .
.
The set (
{cal X} = left{ x in mathbf{R}^n : f_i(x) le 0, ;; i=1,ldots, m right} ) is called the feasible set. Any 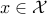 is called feasible (with respect to the specific optimization problem at hand).
is called feasible (with respect to the specific optimization problem at hand).
Alternate representations
Sometimes, the model is described in terms of the feasible set, as follows:
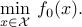
The representation is not strictly equivalent to the more explicit form (ref{eq:math-program-CVXPBS}), since the set 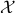 may have several equivalent representations in terms of explicit constraints. (Think for example about a polytope described by its vertices or as the intersection of half-spaces.)
may have several equivalent representations in terms of explicit constraints. (Think for example about a polytope described by its vertices or as the intersection of half-spaces.)
Also, sometimes a maximization problem is considered:
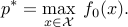
Of course, we can always change the sign of  and transform the maximization problem into a minimization one. For maximization problem, the optimal value
and transform the maximization problem into a minimization one. For maximization problem, the optimal value 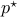 is set by convention to
is set by convention to 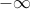 if the problem is not feasible.
if the problem is not feasible.
Feasibility problems
In some instances, we do not care about any objective function, and simply seek a feasible point. This so-called feasibility problem can be formulated in the standard form, using a zero (or constant) objective.
Convex optimization problems
Standard form
The problem
![displaystylemin_x : f_0(x) ~:~ begin{array}[t]{l} f_i(x) le 0,quad i=1,cdots, m, Ax = b, quad i=1,cdots,p, end{array}](https://inst.eecs.berkeley.edu/~ee227a/fa10/login/eqs/7020264096316324256-130.png)
is called a convex optimization problem if the objective function  is convex; the functions defining the inequality constraints
is convex; the functions defining the inequality constraints 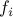 ,
, 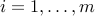 are convex; and
are convex; and 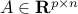 ,
, 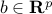 define the affine equality constraints. Note that, in the convex optimization model, we do not tolerate equality constraints unless they are affine.
define the affine equality constraints. Note that, in the convex optimization model, we do not tolerate equality constraints unless they are affine.
Examples:
-
Least-squares problem:
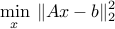
where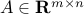 ,
, 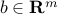 , and
, and 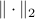 denotes the Euclidean norm. This problem arises in many situations, for example in statistical estimation problems such as linear regression. The problem dates back many years, at least to Gauss (1777-1855), who solved it to predict the trajectory of the planetoid Ceres.
denotes the Euclidean norm. This problem arises in many situations, for example in statistical estimation problems such as linear regression. The problem dates back many years, at least to Gauss (1777-1855), who solved it to predict the trajectory of the planetoid Ceres.
-
Linear programming problem:
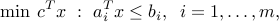
where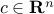 ,
, 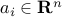 ,
, 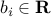 (
(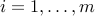 ). This corresponds to the case where the functions
). This corresponds to the case where the functions 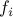 (
(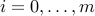 ) in (ref{eq:convex-pb-L4}) are all affine (that is, linear plus a constant term). This problem was introduced by Dantzig in the 40's in the context of logistical problems arising in military operations. This model of computation is perhaps the most widely used optimization problem today.
) in (ref{eq:convex-pb-L4}) are all affine (that is, linear plus a constant term). This problem was introduced by Dantzig in the 40's in the context of logistical problems arising in military operations. This model of computation is perhaps the most widely used optimization problem today.
-
Quadratic programming problem:
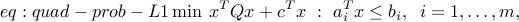
where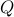 is symmetric and positive semi-definite (all of its eigenvalues are non-negative). This model can be thought of as a generalization of both the least-squares and linear programming problems. QP's are popular in many areas, such as finance, where the linear term in the objective refers to the expected negative return on an investment, and the squared term corresponds to the risk (or variance of the return). This model was introduced by Markowitz (who was a student of Dantzig) in the 50's, to model investment problemsfootnote{Markowitz won the Nobel prize in Economics in 1990, mainly for this work.}.
is symmetric and positive semi-definite (all of its eigenvalues are non-negative). This model can be thought of as a generalization of both the least-squares and linear programming problems. QP's are popular in many areas, such as finance, where the linear term in the objective refers to the expected negative return on an investment, and the squared term corresponds to the risk (or variance of the return). This model was introduced by Markowitz (who was a student of Dantzig) in the 50's, to model investment problemsfootnote{Markowitz won the Nobel prize in Economics in 1990, mainly for this work.}.
Optimality
Local and global optima
A feasible point 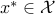 is a globally optimal (optimal for short) if
is a globally optimal (optimal for short) if 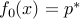 .
.
A feasible point 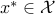 is a locally optimal if there exist
is a locally optimal if there exist 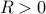 such that
such that 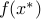 equals the optimal value of problem (ref{eq:convex-pb-L4}) with the added constraint
equals the optimal value of problem (ref{eq:convex-pb-L4}) with the added constraint 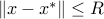 . That is,
. That is, 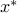 solves the problem ''locally''.
solves the problem ''locally''.
For convex problems, any locally optimal point is globally optimal.
Indeed, let 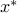 be a local minimizer of
be a local minimizer of  on the set
on the set 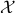 , and let
, and let 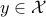 . By definition,
. By definition, 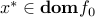 . We need to prove that
. We need to prove that 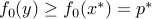 . There is nothing to prove if
. There is nothing to prove if 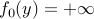 , so let us assume that
, so let us assume that 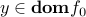 . By convexity of
. By convexity of  and
and 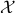 , we have
, we have 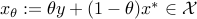 , and:
, and:
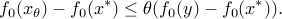
Since 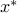 is a local minimizer, the left-hand side in this inequality is nonnegative for all small enough values of
is a local minimizer, the left-hand side in this inequality is nonnegative for all small enough values of 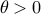 . We conclude that the right hand side is nonnegative, i.e.,
. We conclude that the right hand side is nonnegative, i.e., 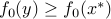 , as claimed.
, as claimed.
Optimal set
The optimal set, 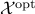 , is the set of optimal points. This set may be empty: for example, the feasible set may be empty. Another example is when the optimal value is only reached in the limit; think for example of the case when
, is the set of optimal points. This set may be empty: for example, the feasible set may be empty. Another example is when the optimal value is only reached in the limit; think for example of the case when 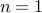 ,
, 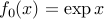 , and there are no constraints.
, and there are no constraints.
In any case, the optimal set is convex, since it can be written (
{cal X}^{rm opt} = left{ x in mathbf{R}^n : f_0(x) le p^ast, ;; x in {cal X} right} . )
Optimality condition
When  is differentiable, then we know that for every
is differentiable, then we know that for every 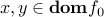 ,
,
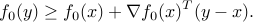
Then 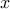 is optimal if and only if
is optimal if and only if
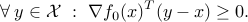
If 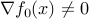 , then it defines a supporting hyperplane to the feasible set at
, then it defines a supporting hyperplane to the feasible set at 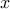 .
.
Examples:
-
For unconstrained problems, the optimality condition reduces to
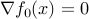 .
. -
For problems with equality constraints only, the condition is that there exists a vector
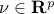 such that
such that
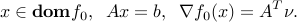
Indeed, the optimality condition can be written as: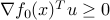 for every
for every 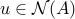 , which is the same as
, which is the same as 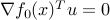 for every
for every 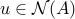 . In turn, the latter means that
. In turn, the latter means that 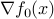 belongs to
belongs to 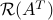 , as claimed. The optimality conditions given above might be hard to solve. We will return to this issue later.
, as claimed. The optimality conditions given above might be hard to solve. We will return to this issue later.
Equivalent problems
We can transform a convex problem into an equivalent one via a number of transformations. Sometimes the transformation is useful to obtain an explicit solution, or is done for algorithmic purposes. The transformation does not necessarily preserve the convexity properties of the problem. Here is a list of transformations that do preserve convexity.
Epigraph form
Sometimes it is convenient to work with the equivalent epigraph form:
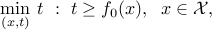
in which we observe that we can always assume the cost function to be differentiable (in fact, linear), at the cost of adding one scalar variable.
Implicit constraints
Even though some problems appear to be unconstrained, they might contain implicit constraints. Precisely, the problem above has an implicit constraint 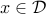 , where
, where 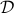 is the problem's domain (
is the problem's domain (
{cal D} := {bf dom} f_0 bigcap_{i=1}^m {bf dom} f_i . ) For example, the problem
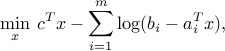
where 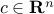 ,
, 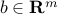 and
and 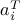 's are the rows of
's are the rows of 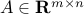 , arises as an important sub-problem in some linear optimization algorithms. This problem has the implicit constraint that
, arises as an important sub-problem in some linear optimization algorithms. This problem has the implicit constraint that 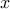 should belong to the interior of the polyhedron
should belong to the interior of the polyhedron 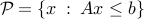 .
.
Making explicit constraints implicit
The problem in standard form can be also written in a form that makes the constraints that are explicit in the original problem, implicit. Indeed, an equivalent formulation is the unconstrained convex problem

where 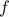 is the sum of the original objective and the indicator function of the feasible set
is the sum of the original objective and the indicator function of the feasible set 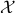 :
:
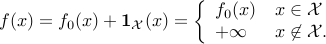
In the unconstrained above, the constraints are implicit. One of the main differences with the original, constrained problem is that now the objective function may not be differentiable, even if all the functions 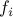 's are.
's are.
A less radical approach involves the convex problem wih one inequality constraint
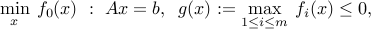
which is equivalent to the original problem. In the above formulation, the structure of the inequality constraint is made implicit. Here, the reduction to a single constraint has a cost, since the function 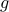 may not be differentiable, even though all the
may not be differentiable, even though all the 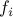 's are.
's are.
The above transformations show the versatility of the convex optimization model. They are also useful in the analysis of such problems.
Equality constraint elimination
We can eliminate the equality constraint 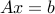 , by writing them as
, by writing them as 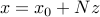 , with
, with 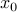 a particular solution to the equality constraint, and the columns of
a particular solution to the equality constraint, and the columns of 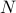 span the nullspace of
span the nullspace of 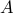 . Then we can rewrite the problem as one without equality constraints:
. Then we can rewrite the problem as one without equality constraints:
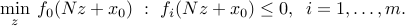
This transformation preserves convexity of the the function involved. In practice, it may not be a good idea to perform this elimination. For example, if 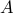 is sparse, the original problem has a sparse structure that may be exploited by some algorithms. In contrast, the reduced problem above does not inherit the sparsity characteristics, since in general the matrix
is sparse, the original problem has a sparse structure that may be exploited by some algorithms. In contrast, the reduced problem above does not inherit the sparsity characteristics, since in general the matrix 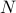 is dense.
is dense.
Introducing equality constraints
We can also introduce equality constraints in the problem. There might be several justifications for doing so: to reduce a given problem to a standard form used by off-the-shelf algorithms, or to use in decomposition methods for large-scale optimization.
The following example shows that introducing equality constraint may allow to exploit sparsity patterns inherent to the problem. Consider
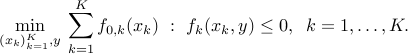
In the above the objective involves different optimization variables, which are coupled via the presence of the ''coupling'' variable 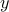 in each constraint. We can introduce
in each constraint. We can introduce 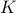 variables and rewrite the problem as
variables and rewrite the problem as
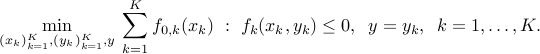
Now the objective and inequality constraints are all independent (they involve different optimization variables). The only coupling constraint is now an equality constraint. This can be exploited in parallel algorithms for large-scale optimization.
Slack variables
Sometimes it is useful to introduce slack variables. For example, the problem with affine inequalities
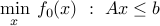
can be written
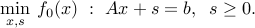
Minimizing over some variables
We may ''eliminate'' some variables of the problem and reduce it to one with fewer variables. This operation preserves convexity. Specifically, if 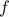 is a convex function of the variable
is a convex function of the variable 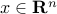 , and
, and 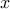 is partitioned as
is partitioned as 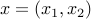 , with
, with 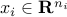 ,
, 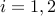 ,
, 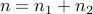 , then the function
, then the function
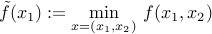
is convex (look at the epigraph of this function). Hence the problem of minimizing 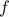 can be reduced to one involving
can be reduced to one involving 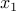 only:
only:
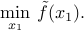
The reduction may not be easy to carry out explicitly.
Here is an example where it is: consider the problem
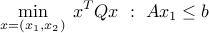
where
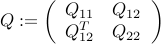
is positive semi-definite, 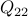 is positive-definite, and
is positive-definite, and 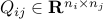 ,
, 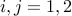 . Since
. Since 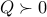 , the above problem is convex. Furthermore, since the problem has no constraints on
, the above problem is convex. Furthermore, since the problem has no constraints on 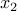 , it is possible to solve for the minimization with respect to
, it is possible to solve for the minimization with respect to 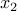 analytically. We end up with
analytically. We end up with

with 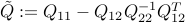 . From the reasoning above, we infer that
. From the reasoning above, we infer that 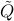 is positive semi-definite, since the objective function of the reduced problem is convex.
is positive semi-definite, since the objective function of the reduced problem is convex.
Complexity
Complexity of an optimization problem refers to the difficulty of solving the problem on a computer. Roughly speaking, complexity estimates provide the number of flops needed to solve the problem to a given accuracy of the objective  . That problem is usually expressed in terms of the problem size, as well as the accuracy
. That problem is usually expressed in terms of the problem size, as well as the accuracy  .
.
The complexity usually refers to a specific method to solve the problem. For example, we may say that solving a dense linear optimization problem to accuracy  with
with 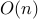 variables and constraints using an ''interior-point'' methodfootnote{This term refers to a class of methods that are provably efficient for a large class of convex optimization problems.} grows as
variables and constraints using an ''interior-point'' methodfootnote{This term refers to a class of methods that are provably efficient for a large class of convex optimization problems.} grows as 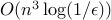 .
.
The complexity of an optimization problem also depends on its structure. Two seemingly similar problem may require a widely different computational effort to solve. Some problems are "NP-hard", which roughly means that they cannot be solved in reasonable time on a computer. As an example, the quadratic programming problem (ref{eq:quad-prob-L1}) seen above is "easy" to solve, however the apparently similar problem obtained by allowing 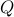 to have negative eigenvalues is NP-hard.
to have negative eigenvalues is NP-hard.
In the early days of optimization, it was thought that linearity was what distinguished a hard problem from an easy one. Today, it appears that convexity is the relevant notion. Roughly speaking, a convex problem is easy. In the next section, we will refine this statement.
Source: https://inst.eecs.berkeley.edu/~ee227a/fa10/login/l_cvx_pbs.html
0 Response to "Why Are Convex Optimisation Problems Considered to Be Easy to Solve"
Post a Comment